As we discussed last month, I thought that we might start out with our Primer on Biostatistics from a clinician’s standpoint. I know that statistics can be daunting for those of you who are like I was – having a dislike of mathematics and not having a clue about statistics. The amazing thing is that you can learn so much about a study simply by reading the tables, the numbers, graphs, and figures. Many readers might just go to the tables and figures if the abstract has gotten their interest. I can still remember one of my professors in graduate school telling us that he only read the abstracts of papers to digest their meaning and rarely did he actually read the entire paper. I am somewhere in between – if the abstract is not interesting, I don’t really care to read the paper. If it is and has some good data to report, I will read the paper and specifically look at the tables and graphs to get a real insight into the methodologies as well as the important results.
All of this, however, presupposes that the reader has a basic understanding of medical statistics and knows what he/she is reading. I can’t say that I really did for all of my training and the first 14 years of practice – a real shortcoming! You need to be an educated consumer of the medical literature in this century if you are to stay abreast of developments. So let’s make it as easy as possible and start with the basics first. Digest the information in this series in small quantities so that it is comprehensible and meaningful. Again, I am a clinician, so things need to be made clear to me in a simplified manner that I can understand. I’ll try to do the same for you.
To Start — Descriptive Statistics
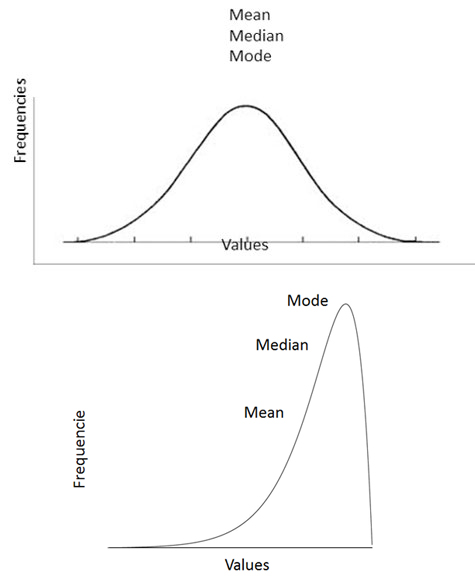
Descriptive statistics will be our starting point because of their basic nature and fundamental importance to a discussion of statistics. Although we haven’t yet discussed Student t-tests, you have obviously heard of this basic analytical method for hypothesis testing. But you very likely do not realize that it is most often used inappropriately. This is because the users (or authors) did not pay attention to the descriptive attributes of their study data. In this regard, t-tests require that the data follows a normal distribution (bell curve or parametric) and not a skewed distribution (non-parametric). See Figure 1 below. Specific to our point at this time, however, a t-test is used to test differences between means of two populations or matched pairs. Aside from frequencies (percentages or crude numbers), measures of central tendencies lie at the heart of descriptive statistics. The three measures of central tendency that describe populations are mean, median, and mode. Most of us are familiar with means– the mathematical average of a sum of values (divided by the count or number of values summed). This is a very simple concept that we have all mastered in grade school. However, the mathematical average value of a population/distribution does not always give an accurate picture of that population.
Figure 1. Normal distribution or “Bell” curve (top). Skewed distribution (bottom) |
|
|
|
Remember that the mean follows the tail – this means that a single skewed or aberrant result way out of line (i.e. excessively large or small) will affect the average value by skewing that average toward that outlier value. While describing the mean is appropriate for a normally distributed population (where the mean lies in the center of the curve), it is not appropriate for a non-parametric dataset (population). For data that is not normally distributed but skewed, it is appropriate to measure the center of the data by its median. The median is defined as the middle value when the numbers are arranged in increasing or decreasing order. For instance, if we have the following five values of 2, 3, 5, 9, and 10, the median or middle value would be 5. This is fine for an odd number of individual values (half are larger and half are smaller), but for an even number of values (datapoints) the median is defined as the average of the two middle values. For instance, in the following data set of six values ( 2, 6, 10, 13, 17, and 20), the average of the two middle values (10 and 13) is 11.5 – thus, it is the median value of this dataset. It best describes the center of this dataset.
The final measure of central tendency is the mode. The mode is described as the most common value occurring in a set of numbers. If we have a set of five prices from five sources for a new statistical calculator, the iCalc, that includes: $150, $155, $150, $160, and $159.50, we can easily see that the mode is $150. This is the value (price) that occurs most frequently from these sources.
The Three Measures of Central Tendency: |
- Mean – the mathematical average of a sum of values
- Median - the middle value when the numbers are arranged in order
- Mode - the most common value occurring in a set of numbers
|
Interestingly, for a perfectly symmetric distribution (Bell curve, normal distribution), the mean, median, and mode will all fall at the center of the curve. For skewed populations, the mean will always follow the tail (outliers) such that it lies on one or the other side of the curve, adjacent at some level to the median value. The mode will usually be found toward the high point of the curve, reflecting the most commonly occurring value. (Figure 2)
| Figure 2. In the normal curve (top), the mean , median, and mode are all at the same point. In the negatively skewed curve below, the three measures of central tendency are at different points (values) along the curve. |
|
 |
|
That’s it for now- we will keep things simple so you can assimilate these concepts. They will be your building blocks for the future. If I can understand statistics, so can you! I have provided references for you below and suggest that you do some reading on your own.
My hope is that you too will be amazed at the Power of Numbers...
See you next time.
Robert Frykberg, DPM, MPH
PRESENT Editor,
Diabetic Limb Salvage
REFERENCES:
- Statistics. Cliffs Notes, Lincoln Nebraska. David Voelker and Peter Orton. 1993
- Online Statistics Education: An Interactive Multimedia Course of Study (https://onlinestatbook.com/)
- Stanton Glantz. Primer of Biostatistics. McGraw – Hill, Inc., New York
We at PRESENT love hearing from you. I would encourage you to share your experience, pearls, and wisdom on this topic, or on any other that you would like to share with our online community via eTalk.
Your continued participation is what makes this Web portal great!
Get a steady stream of all the NEW PRESENT Podiatry
eLearning by becoming our Facebook Fan.
Effective eLearning and a Colleague Network await you. |
 |
Grand Sponsor |
 |
|
| Diamond Sponsor |
 |
|
| |
|
Major Sponsors |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|