I teach a number of students (as well as my Residents) throughout the course of the academic year, primarily in our clinics. Part of the clinical rotation includes a weekly Journal Club – I think this is an essential part of the rotation, since it gives us the opportunity to discuss current literature. It also gives me the opportunity to assess students' knowledge of the literature and their comprehension of it. To this end, I am particularly interested in their understanding of basic medical statistics such as we have been discussing over the last several months. (I'm still surprised how many Residents and students do not avail themselves of these free eZines)! Almost invariably, their incomprehension of statistical concepts comes to light very quickly. When I ask what the statistical tests mean or what is a p-value or what is the definition of positive predictive value in term of probabilities, they usually do not really understand what they are reading (and regurgitating). Then I ask, "How can you understand the meaning of the data presented if you do not understand these basic statistical methods and concepts?" Again, it goes back to a lack of focus on what is important in the training of the modern doctor (and believe me, it is not how many type of bunion operations one can recall!). Hence, the rationale for this clinician's guide to basic statistical concepts (from an old clinician).
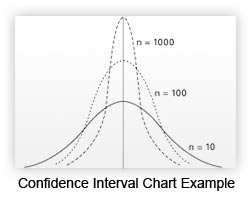 |
Last month we discussed the all-important and poorly understood p-value and that magical "p<0.05" – the benchmark for accepting the statistical significance of a hypothesis test, a difference between means, or differences between two groups. Yes, you must all understand what the p-value represents and I'll refer you back to our April eZine for that information. While I won't rehash that entire exercise, remember that the "p" stands for probability and probabilities go from zero to one (0 – 1.0). You can also consider that a probability of 1 is equivalent to 100 percent (100%). That is, 100 out of 100 times that a test is performed, it will give the same result. There are very few 100% probabilities in this world except for death (not even taxes are 100% these days!). Probabilities usually lie in the range of 0 to 1 depending on the test. The best example is a coin toss- 50% probability of landing on heads and 50% probability of tails if the coin is tossed enough times. Therefore, if p<0.05 (<5%), what about the other 95% of a distribution (of probabilities of different values)? We only accept statistical significance of a difference in means if the probability (chance) of having the same result or larger between two measures or tests is less than 5% (p<0.05). Now in small populations, there might be a lot of overlap in two compared groups, simply because the number of individual data points (values) can be spread out due to a large standard deviation. Take weights of two populations for instance (for that matter you can take just one population to make the same example). First, take the weights of 10 Iowa farmer's daughters aged 16 years old. Those weights might range from 100 pounds to 200 pounds and in a small sample, might actually have a mean of 145 lbs. This mean would be a sample mean or point estimate and you would have little confidence in this value. Because of the small numbers, there is wide variance and the curve would not be our nice normal bell curve (it would be skewed). But we realize that if we took the entire population of 16 year old Iowa farmer's daughters, we could estimate the true mean of this population. But we really can't do this, so we estimate sample means (the more in the sample the better). By increasing the numbers, we would get a different value that would actually be closer to the population true mean (more power to detect this mean because of increased number of data points and decreased variation or standard deviation). In this scenario where 100 girls were weighed, we obtained a sample mean weight of 157lbs, with a range of values around the mean. We could then statistically compute a 95% confidence interval (CI) around this mean (or many other type of parameters) that would contain the true population mean 95% of the time. Stated otherwise, we would determine that with 95% probability (or confidence), the population mean would lie in the range of (for example purposes) 126 lbs (lower bound) to 179 lbs (upper bound). The estimate for the population mean weight would be written: 157 lbs, 95% CI (126-179). So 5% of the time, the true population mean would not be within this interval (remember, probabilities within a normal distribution must equal 100%). There is a statistical calculation for determining 95% CI of means based on normal populations and the standard deviation of samples, but this is beyond our purposes here and beyond my ability to recollect at this point (but you can refer to the citations below for further clarification).
In most of the literature we read in which groups are compared for some value such as means or to determine measures of association (Odds Ratios=OR), we are provided a value and its statistical significance to determine if the two groups are really different or if they overlap too much to be statistically different. Let's use means in this case, since it is easy to understand. If two populations are the same, the difference between their mean weights will be 0. If the estimate of the difference is zero, then they are not statistically different and there is no statistical significance between their sample mean weights. Therefore, the 95% CI around that mean difference between the groups will include 0 within a given lower and upper bound for the true population difference. And the p-value must be greater than 0.05, because with 95% probability the true difference between mean weights lies in a range that also includes 0. Back to our Iowa girls with a mean sample weight of 157 lbs. Let's compare them to a population of 16 year old Mississippi girls where the mean weight was only 150 lbs. We can do a t-test to determine the significance of the difference between the mean weights and we will obtain a mathematical difference of 7 lbs. But based on sample sizes and standard deviations and errors of the means (measures of variability) we find that there is really no significant difference between these means. Why? Because the computed 95% CI for the true difference was (for example): -2 to 12.5 lbs. Now this range certainly contains the estimated difference of 7 lbs, but it also contains a value of 0 : the confidence interval crosses 0: it goes below (-2) and above (12.5) zero, the null value for the difference in mean weights. So p>0.05 automatically because it cannot be a significant difference between these two groups when the 95% CI contains 0 between the lower and upper bounds. Now that you know this, start looking at the 95% CI ranges when you read papers. Don't even look at the p-values. You will know all non-significant differences between means whenever you see the confidence interval crossing from a negative value, past 0, and then to a positive value. If the 95% CI contains all positive values (i.e. 1.2 -13.7) and does not cross zero, it is indeed a significant difference between these means. Similarly, if the lower and upper bounds both lie below zero (i.e. -4 to -.5), the difference is significant as well (p<0.05).
Although I might have thoroughly confused you by now, just remember the basic points about the 95% Confidence Interval: it represents a range within which the true population value lies, based upon your sample estimates. In other words, with 95% probability the true value lies in the given range. If that range contains zero, there might actually be no difference between the two study groups and the p-value for this difference must be >0.05. 95% CI is important because it also gives you the stability of your estimates- a very wide 95% CI reflects an unstable estimate (much variability in your sample) while a narrow range provides a more stable estimate based on a larger sample size. Nonetheless, both can be significant values – as long as they do not cross zero.
Sorry for the confusion – please try to glance at the references provided. It took me at least 5 times to read and understand these concepts – I think.
My hope is that you too will be amazed at the Power of Numbers...
See you next time.
Robert Frykberg, DPM, MPH
PRESENT Editor,
Diabetic Limb Salvage
Suggested References:
- Statistics. Cliffs Notes, Lincoln Nebraska. David Voelker and Peter Orton. 1993
- Online Statistics Education: An Interactive Multimedia Course of Study (https://onlinestatbook.com/)
- Stanton Glantz. Primer of Biostatistics. McGraw – Hill, Inc., New York
- Theodore Colton. Statistics in Medicine. Little, Brown, and Company. Boston
We at PRESENT love hearing from you. I would encourage you to share your experience, pearls, and wisdom on this topic, or on any other that you would like to share with our online community via eTalk.
Get a steady stream of all the NEW PRESENT Podiatry
eLearning by becoming our Facebook Fan.
Effective eLearning and a Colleague Network await you. |
 |
This ezine was made possible through the support of our sponsors: |
Grand Sponsor |
 |
|
| Diamond Sponsor |
 |
|
| |
Major Sponsors |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|